Для оценки уровня упорядоченности процессов вычисляется так называемый «параметр хаотизации»:
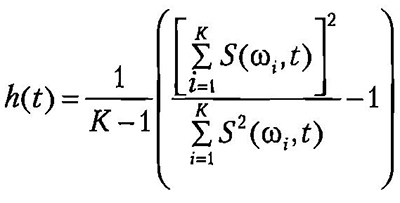
Нулевое значение параметра соответствует наличию одной спектральной линии (т.е. ряд состоит из одной синусоиды), а единичное — случаю белого шума. Таким образом, области повышенных значений параметра могут свидетельствовать о моментах повышенной «хаотизации» процесса (например, при распаде неустойчивости с образованием хаотических колебаний), а минимальные значения параметра — большей его «упорядоченности», например, при синхронизации различных ритмов.
Необходимо отметить, что данный параметр реагирует на присутствие во временных рядах резких всплесков и выбросов, что требует определенной осторожности при интерпретации результатов обработки. Пакет программ, включающих описанные выше процедуры, был написан С.И. Александровым.
Оценивая возможности преобразования Фурье для исследования временных рядов рассматриваемых ниже процессов, отметим, что оно обладает способностью фокусировать в точку «размазанную» по времени информацию о периодичности функции при переходе из временной области в частотную.
Это достигается за счет того, что ядро преобразования Фурье, т.е. функция, не локализовано во времени, но имеет предельную локализацию в частотной области. Это обстоятельство делает преобразование Фурье прекрасным инструментом для изучения процессов, свойства которых не меняются со временем. Однако оно же делает преобразование Фурье плохим методом для исследования функций, характеристики которых эволюционируют во времени.
Для устранения этого недостатка преобразование Фурье локализуют на промежутках конечной длины, что позволяет получить эволюцию спектра во времени. Важно подчеркнуть, что окно преобразования имеет постоянную ширину и увеличение разрешения во временной области приводит к уменьшению частотного разрешения. Таким образом, естественное для анализа нерегулярных сигналов стремление повысить временное разрешение всегда приводит к уменьшению разрешающей способности в области частот.
К этому следует добавить, что при использовании оконного преобразования возникает проблема выбора ширины окна во временной области. Слишком широкое окно может обеспечить разумное представление низкочастотных компонентов ряда, но его ширина будет избыточной для гармоник с высокой частотой, в результате чего все интересные нерегулярности в высокочастотной области спектра сгладятся (рис. 1в). Наоборот, достаточно узкое окно даст возможность изучить вариации во времени высокочастотных компонентов, но оно не будет адекватным для низкочастотных гармоник (рис. 1г).
Если сделать оконную функцию зависящей от частоты так, чтобы для низких частот окно становилось шире, а для высоких уже, то оконное преобразование Фурье трансформируется в вейвлет-преобразование. Преобразование Фурье — это корреляция между исходным рядом и волной, которая характеризуется значением частоты, поэтому оно является функцией одной переменной. Вейвлет — это корреляция между исходным рядом и всплеском, который характеризуется масштабом и локализацией на оси времени. Поэтому вейвлет-преобразование зависит от двух аргументов — масштаба вейвлета и его положения на оси времени.
Вейвлет-преобразование не просто «режет» исследуемый объект на куски, а выделяет из него компоненты разных масштабов, каждый из которых анализируется с той степенью детальности, которая соответствует его масштабу.
Интегральное вейвлет-преобразованием функции имеет вид
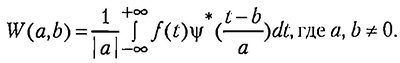
Функция называется вейвлетом (анализирующим, базисным или материнским), символом * обозначена процедура комплексного сопряжения.
Параметр b задает временную локализацию вейвлета и называется сдвигом. Параметр а определяет размер вейвлета и называется масштабом. Его аналогом в Фурье-анализе является период (частота) гармонического колебания. Понятие масштаба — более широкое (хотя и менее наглядное), чем понятие периода. Связано это с тем, что в Фурье-преобразовании функциональный вид ядра преобразования зафиксирован раз и навсегда, в то время как вейвлет-преобразование одной и той же функции можно получить с помощью различных базисных вейвлетов, т.е. в разных системах масштабов.
В качестве инструмента анализа динамики рассматриваемых рядов мы использовали широко известные и используемые чаще других при частотно-временном анализе вейвлет-функции Morlet
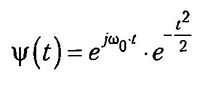
и DOG (от англ. — difference of gaussians):
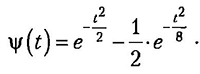
Выбор этих двух вейвлетов объясняется тем, что они по-разному локализованы в пространственно-временной области и могут взаимно дополнять друг друга. Для вейвлета DOG характерна относительно высокая степень локализации как по времени, так и по частоте. Вейвлет Morlet не так сильно локализован во времени, но его разрешающая способность в области масштабов больше, чем у DOG-вейвлета.
Перемещая и масштабируя базисные вейвлет-функции в пределах области определения сигнала, получаем набор вейвлет-коэффициентов, распределение которых в координатах период-время является результатом вейвлет-анализа (на оси ординат откладываются периоды, а на оси абсцисс — календарное время в часах, сутках, годах и др.). Программа для расчета вейвлет-коэффициентов была написана Е.И. Динабургом и Е. Кугаковой в среде Matlab.
Характерной особенностью анализирующих вейвлетов является частотно-временная локализация. Вейвлет Морле всегда охватывает несколько периодов и не лучшим образом локализован во времени. Кроме того, близкие по частоте гармоники могут не разрешаться с помощью вейвлета Морле без потери временного разрешения. Не найдя достаточно весомых преимуществ вейвлета Морле над СВАН-ом при анализе фактических рядов, в предметных статьях мы использовали этот вейвлет очень ограниченно.
Вейвлет-функция DOG характеризуется хорошим временным разрешением. Этот вейвлет существенно отличается от нуля в пределах малых временных и частотных интервалов и очень мало отличается от него вне этих интервалов. На рис. 2 можно увидеть другие примеры результатов вейвлет-анализа некоторых заранее известных функций, а на рис. 3,4 — фактических рядов данных.

Рис. 2. Примеры результатов вейвлет-анализа некоторых известных сигналов вейвлетом DOG. График вейвлет-функции DOG (а), графики анализируемых сигналов (б, г, е, з), результаты вейвлет-анализа этих функций (в, д, ж, и)
Посмотрим, как соотносятся графики вейлет-функции (а), анализируемой функции f(x) (б) и результата вейвлет-анализа W(a, b) в координатах периода T и времени t (а). Анализируемый сигнал состоит из трех сменяющих друг друга кнаэиисриодичсских функций: одного периода Т = 130, двух периодов T = 30 и восемнадцати периодов Т = 5. В точках 1 и 2 (б) вейвлет хорошо совпадает с анализируемой функцией, значения функции W(a, b) максимальны, на графике это некая область точек, которую можно описать центром t и радиусом At (центром T и радиусом AT). Так, точкам 1-6 на графике анализируемой функции (б) соответствуют точки 1-6 — на масштабно-сдвиговой плоскости (а).