Обработка временных рядов данных проводилась одними и теми же унифицированными способами анализа нестационарных процессов, в значительной мере по программам С.И. Александрова. Использовались различные методы анализа: спектрально-временной, спектральный, корреляционный (в том числе, в скользящем временном окне), в ряде случаев вейвлет-анализ, способ, основанный на расчетах структурных функций и др.
Мы опустим описание стандартных процедур предварительной обработки, таких как интерполяция, исключение тренда (эта процедура автоматически выполняется при различных приемах спектрального и корреляционного анализа), фильтрация временных рядов и др. Сначала рассмотрим на примере аналитически заданного сигнала (рис. 1а) основные процедуры, использованные нами для анализа фактических рядов данных, относящихся к различным природным процессам.

Рис. 1. Пример использования основных приемов обработки временных рядов. Исследуемый сигнал (а), амплитудный спектр этого сигнала (б), СВАН-диаграммы (в, г) с шириной окна анализа 80% и 20% от длины ряда соответственно, результаты вейвлет-анализа с базисными функциями Morlet (д) и DOG (е), график структурной функции всего сигнала (ж), график скользящей структурной функции (з) с окном анализа 24 точки и шагом 1 точка, справа дана ориентировочная шкала в точках исследуемого ряда
Исследуемый сигнал (длиной 100 точек) представляет собой сумму двух квазигармонических сигналов: один — с периодом Т = 83, другой состоит из нескольких частей — первые 40 точек с периодом Т = 5, следующие 30 — с Т = 20, последние 30 — с Т = 5.
На амплитудном спектре хорошее частотное разрешение характерно для сигналов достаточной длины, включающих несколько периодов, короткие сигналы (с T = 20 и 83) разрешены значительно хуже.
На СВАН-диаграмме (а) окно анализа, равное 80% от длины ряда, обеспечивает хорошее представление низкочастотных компонентов сигнала (все гармоники сигнала различимы, но наиболее выражена гармоника с периодом T = 83). Но такая ширина окна избыточна для гармоник с высокой частотой, нерегулярности в высокочастотной области спектра не видны. Достаточно узкое окно анализа, равное 20% от длины ряда, дает хорошее разрешение по времени высокочастотных компонентов, по в данном случае не выражена самая низкочастотная гармоника сигнала с периодом Т = 83.
Результатом вейвлет-анализа является поверхность, которую на приведенных рисунках мы представили в виде изолиний разных оттенков, вертикальная шкала палитры приведена справа. На всех последующих рисунках палитра оттенков та же. В тематических главах результаты вейвлет-анализа представлены оттенками серого, при этом усиление тона означает рост значений функции W(a,b). Присутствие доминирующей частоты в вейвлет-функции Morlet позволяет варьировать избирательностью функции в частотной области. В данном случае все частоты анализируемого сигнала разрешены. Анализ сигнала с помощью вейвлета DOG дает хорошее разрешение по времени всех гармоник.
Возможность выделения таких длиннопериодных компонентов сигнала, как в нашем случае гармоника с периодом 83, с помощью двух описанных процедур обычно ставится под сомнение. Более уверенно о них можно судить, если дополнительно проанализировать сигнал с помощью структурной функции. Максимум структурной функции (около 42) соответствует половине периода наиболее длиннопериодной компоненты рассматриваемого сигнала. На графике структурной функции хорошо выделяются гармоника с Т = 20 и короткопериодная гармоника с Т = 5.
Короткопериодная гармоника (Т = 5) хорошо видна на графике скользящей структурной функции, здесь же можно проследить вариации во времени низкочастотных составляющих сигнала. Графики скользящей структурной функции построены таким образом, что каждая последующая кривая смещена относительно предыдущей па один и тот же временной шаг. Если при переходе от одной кривой к другой периоды и амплитуды ритмов не меняются, кривые располагаются строго друг над другом и не пересекаются. Если происходит изменение амплитуд какого-то ритма, визуально это выглядит как чередование темных и светлых пятен в месте, соответствующем периоду данного ритма.
Увеличение доли длиннопериодных ритмов отмечается на графике более темной, по сравнению с общим тоном,секущей с положительным трендом в сторону длинных периодов, соответственно уменьшение их доли — положительным трендом в сторону коротких периодов. Каждая кривая — результат анализа в заданном окне. Окно выбирается исходя из следующих соображений: оно должно более чем в два раза превышать интересующий интервал периодов, вместе с тем не быть слишком большим.
В данном случае окно анализа составляет 24 точки, т.е. нижний график структурной функции по времени соответствует 25-й точке ряда. 15 последующих графиков абсолютно одинаковы (хорошо выделяются периоды 5 и кратный ему 10) и смещены друг относительно друга на 0.5 для лучшего зрительного восприятия. Начиная с 41-й точки ряда (16 график) наблюдается перестройка ритмической структуры, гармоника с периодом 5 исчезает, сигнал на этом отрезке представлен суммой гармоник с периодами 20 и 83, которые выходят за пределы рассматриваемого окна анализа. Тридцатью графиками выше появляется гармоника с периодом 5 и кратными ему.
Затем — несколько примеров, демонстрирующих результаты вейвлет-анализа некоторых аналитически заданных сигналов и фактических рядов данных, которые, на наш взгляд, помогут читателю, незнакомому с этим методом, более свободно ориентироваться в представленном в предметных статьях материале.
Спектральный анализ
Для анализа гармонических составляющих и выявления периодических вариаций (ритмов) используются процедуры построения оценок спектральной плотности процессов (с предварительным исключением тренда). На оси абсцисс (рис. 1б) обозначаются частоты в циклах в единицу времени (например, в час, в год или в млн лет). Разрешающая способность по частоте соответствует частотному шагу анализа
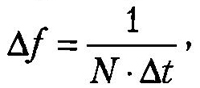
где N — количество отсчетов временного ряда и At — временной интервал между соседними отсчетами.
Доверительные интервалы для выделяемых спектральных пиков строятся исходя из величины спектральной среднеквадратичной погрешности.
Спектрально-временной анализ известен давно и применяется в геофизике, например, для анализа сейсмограмм. Использование процедуры спектрального анализа в скользящем временном окне позволяет проводить изучение нестационарных временных рядов. Результаты представляются в виде диаграмм распределения спектральных амплитуд.
На оси абсцисс откладывается календарное время (в часах, сутках, годах и др.), соответствующее центру скользящего временного окна, на оси ординат — значения частот в циклах в единицу времени или соответствующие периоды (ось ординат равномерна по частотам и, следовательно, неравномерна по периодам).
Каждый вертикальный столбец представляет собой амплитудный спектр Фурье, рассчитанный в заданном скользящем временном окне. Более сильная зачерненность на диаграммах соответствует большим спектральным амплитудам, значения амплитуд представлены шкалой уровней, помещенной около диаграммы. Повторяемость или устойчивость доминирующих ритмов выражается в виде более или менее протяженных зачерненных полос. По этому признаку также можно судить о степени упорядоченности процесса.
Длина окна выбирается исходя из требований получить данные о гармониках в наиболее широком частотном диапазоне с учетом необходимой детальности и фактического частотного состава процесса (рис. lв, г). В итоге получаем наборы диаграмм для разных частотных и временных окон. На них видно, какими ритмами характеризуется тот или иной процесс, каковы их амплитуды и степень устойчивости, как одни ритмы сменяются другими, пропадают или возникают.